PyFinPO - Python Financial Portfolio Optimization Library

PROJECTS · QUANTITATIVE FINANCE

Quant Finance, Portfolio Optimization

450h

Jan. 2024 - Present

INTRO

Project Description

Welcome to PyFinPO, my personal library for Financial Portfolio Optimization in Python.

PyFinPO is a simplified abstraction of other Python libraries for Portfolio Optimization (PyPortOpt, skfolio, scikit-learn, cvxpy...), aiming to provide a structured, direct and extensible infrastructure to perform Financial Portfolio Optimization.

SKILLS

Fields of Expertise

Quantitative Research:

Portfolio Optimization:

Asset Forecasting/Prediction (Expected Return Models, Risk Models…):

Coding (Python):

· · ·

Complexity: ★★★★★

Tools: Python

Project Type: Personal Project

01

Introduction __________

Project Introduction

Chapter 1 -

__ INTRO

When I first set out to develop a Portfolio Optimization Library in Python, my goal was simple: to gain a deep understanding of portfolio theory and its main methods. Building everything from scratch felt like the best way to learn the nuances of the different models, approaches, estimators... and their implementations.

However, as I started exploring the existing Portfolio Optimization libraries in Python, I discovered that there are already VERY GOOD resources available for free (see list below). I quickly came to the realization that it made no sense to implement my own portfolio tool from scratch having all those open-source libraries available –tested and improved through user feedback– that already included most of the Portfolio Optimization tools needed. Reinventing the wheel no longer seemed practical or efficient.

So I changed my mind. Instead of creating yet another standalone library, I decided that in order to understand the nuances of Portfolio Optimization, it would make more sense for me to build a centralized library which organizes the different functionalities available in other open-source libraries under a single, cohesive API. By integrating their strengths with an intuitive high-level interface, this tool could help me (and potentially other users) to seamlessly access the best functionalities each library has to offer without needing to master multiple APIs.

Additionally, I decided to prioritize modularity and extensibility, making extremely easy to add new proprietary models and integrate them in the buit-in API with minimal effort.

In a nutshell, I defined 3 main principles for the project: unified structure, intuitive use, and scalable modularity.

__ INTRO

Unified PO
Functionalities

Intuitive Use

To unify the different Portfolio Optimization functionalities offered in other libraries under a common, structured API.

To provide an intuitive, high-level interface to perform Portfolio Optimization with Python.

Scalable Modularity

To offer a MODULAR and EXTENSIBLE tool which anyone can use to build proprietary models and feed them into the created API structure to leverage the already implemented functionalities in existing libraries.

Project

Motivation

Project

Objectives

02

Content __________

Content & Structure

Chapter 2 -

Content

03

Features __________

PyFinPO Features

Chapter 3 -

___ PYFINPO FEATURES

Overview of

Portfolio Optimization Problem

Portfolio optimization, as formalized by Harry Markowitz in his seminal 1952 paper "Portfolio Selection," revolutionized investment theory by introducing a systematic and quantitative framework to allocate capital among all the available assets. Markowitz demonstrated that by combining securities with differing expected returns and volatilities, investors can construct portfolios that either minimize risk for a given return or maximize return for a specific level of risk. These optimal portfolios form the efficient frontier, a cornerstone of what is now known as Modern Portfolio Theory (MPT).

At the heart of Markowitz’s framework is mean-variance optimization, which requires two key inputs: estimates of expected returns and a covariance matrix to capture asset interdependencies. While the model provides a theoretically optimal solution, its practical application is limited by the difficulty in accurately forecasting these inputs. Historical data is often used as a proxy, though this approach sacrifices the theoretical guarantees of precision.

Advancements in portfolio optimization have expanded upon these ideas, introducing diverse objective functions and measures of risk such as maximizing Sharpe ratios or minimizing Conditional Value at Risk (CVaR). Constraints such as budget limits, sector exposure, or regulatory requirements are incorporated to reflect real-world considerations.

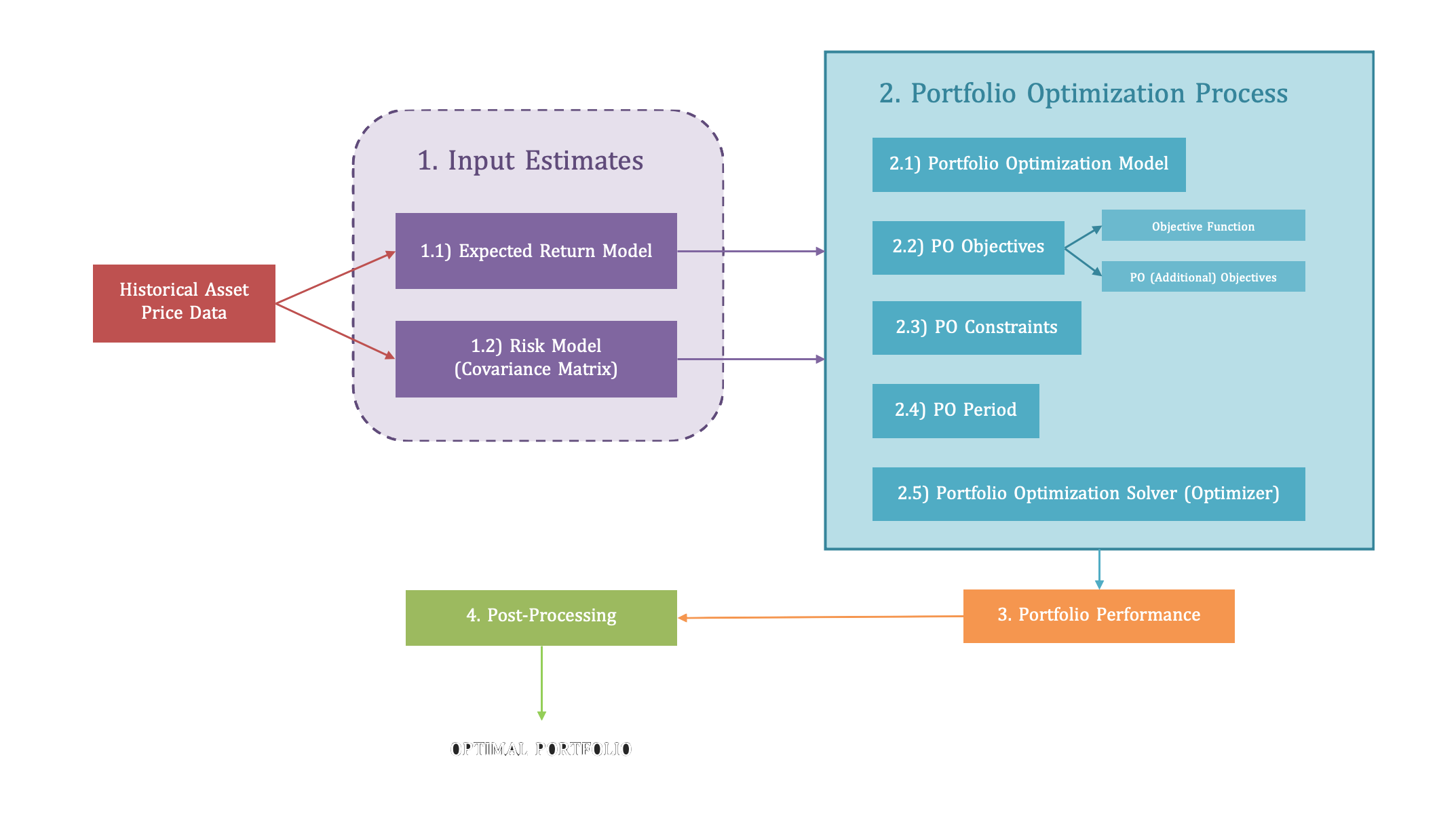
Building from the basic steps of Portfolio Optimization Theory, we can divide portfolio optimization process in 4 main steps, each with their own sub-steps. These are depicted in the Figure below, and fully detailed in the following section.

Four Features.

One Single Library.

1

3

__ Feature I

Input
Estimates

Input estimates aim to forecast the expected return and risk of portfolio securities, to be used as inputs for portfolio optimization.

__ Feature III

__ Feature II

Portfolio
Optimization

Once the input estimates are determined, we can proceed with the portfolio optimization process, which is divided in 5 main steps.

__ Feature IV

Portfolio
Post-Processing

Finally, with the Portfolio Post-Processing module we can generate portfolio outputs and graphics in a user-friendly format.

Portfolio
Performance

Once an optimal portfolio is generated, we can analyze the performance achieved in benchmark key metrics and ratios.

2

4

PyFinPo library offers 4 main functionalities, aggregated under a single, unified API.

__ PYFINPO FEATURE I

3.1

Input Estimates

3.1.1

Every serious Portfolio Optimization model requires of a good proprietary method to properly forecast expected returns as accurately as possible.

The tables below summarize some of the most relevant expected return models found in literature. They are classified by model type, including references to documentation for all of the models and which of them are currently implemented in PyFinPO.

I) Historical Return Models

3.1.1

Model Tag Model Name Documentation Implementation
mh_rm Mean Historical Return Model (aka Empirical Returns) PyPortOpt mh_rm.py
ewmh_rm Exponentially Weighted Mean Return Model PyPortOpt ewmh_rm.py
mceq_rm Market Cap Equilibrium Expected Return Model skfolio To be implemented
eqweq_rm Equal Weight Equilibrium Expected Return Model skfolio To be implemented

II) Economic & Factor Models

Model Tag Model Name Documentation Implementation
capm_rm Capital Asset Pricing Return Model (Equilibrium) PyPortOpt capm_rm.py
apt_rm Arbitrage Pricing Theory (APT) Return Model See docs To be implemented
fama_factor_rm Fama-French Three-Factor Return Model See docs To be implemented
multi_factor_rm Multi-Factor Return Models skfolio To be implemented

III) Statistical / Machine Learning Models

Model Tag Model Name Documentation Implementation
Regression-Based Return Models
ols_rm Ordinary Least Squares (OLS) Regression Model Wikipedia - OLS To be implemented
stacking_rm Stacked Generalization Return Model scikit-learn - StackingRegressor To be implemented
Shrinkage Estimators
shrinkage_rm Shrinkage Return Models Estimators skfolio - Expected Return Shrinkage To be implemented
shrinkage_rm.james_stein Shrinkage Return Models - James-Stein skfolio - Expected Return Shrinkage To be implemented
shrinkage_rm.bayes_stein Shrinkage Return Models - Bayes-Stein skfolio - Expected Return Shrinkage To be implemented
shrinkage_rm.bop Shrinkage Return Models - Bodnar Okhrin Parolya skfolio - Expected Return Shrinkage To be implemented
Bayesian Models
black_litterman_rm Black Litterman Model (return + risk model) PyPortOpt - Black-Litterman black_litterman_rm.py
bayesian_ridge_rm Bayesian Ridge Regression Model Bayesian Predictive Return Distributions To be implemented
Time-Series Forecasting Return Models
arima_rm ARIMA (AutoRegressive Integrated Moving Average) Model Wikipedia - ARIMA To be implemented
Supervised ML Models
svr_rm Support Vector Regression (SVR) Model scikit-learn - SVR To be implemented
ensemble_rm Ensemble Return Model (Weighted Average of Multiple Models) scikit-learn - Ensemble Methods To be implemented
Neural Networks
lstm_rm Long Short-Term Memory (LSTM) Model Wikipedia - LSTM To be implemented

IV) Hybrid Models

Model Tag Model Name Documentation Implementation
Hybrid Models
hybrid_capm_arima Hybrid CAPM + ARIMA Return Model Wikipedia - CAPM, Wikipedia - ARIMA To be implemented
hybrid_bl_lstm Hybrid Black-Litterman + LSTM Return Model PyPortOpt - Black-Litterman, Wikipedia - LSTM To be implemented
hybrid_factor_svr Hybrid Factor Model + SVR Return Model skfolio - Factor Model, scikit-learn - SVR To be implemented
bayesian_lstm_rm Hybrid Bayesian + Neural Network Return Model Bayesian Predictive Return Distributions, Wikipedia - LSTM To be implemented

___ INPUT ESTIMATE 1

__ Input Estimate 1

Expected Return Models

Providing good estimates of asset returns is one of the most important parts of Portfolio Optimization. The objective of Expected Return Models is to estimate the future expected return for each of the assets in the investment universe, during the investment horizon that is subject to optimization.

3.1.2

__ Input Estimate 2

Risk
Models

Same as Return Models, Risk Models provide estimates for the risk of portfolio securities. Most portfolio optimization models will only need as input for risk an estimate for the covariance matrix of the assets in the investment universe.

3.1

Same as with the return models, we will also need to provide a risk model as input for the portfolio optimization. In this case, and although many different risk metrics can be chosen as objective for optimization, most portfolio optimization models will only need as input for risk an estimate for the covariance matrix of all the assets in the investment universe.

As exposed in [1], risk models are often more important than expected return models because historical variance is generally a much more persistent statistic than mean historical returns. In fact, research by Kritzman et al. (2010) suggests that minimum variance portfolios, formed by optimising without providing expected returns, actually perform much better out of sample.

In order to estimate the covariance matrix, several estimators are proposed in the PyFinPO library:

I) Covariance Estimators

Model Tag Model Name Documentation Code
Covariance Estimators
sample_cov Sample Covariance Risk Model RiskModels.md sample_cov.py
empirical_cov Empirical Covariance (Max Likelihood Covariance Estimator) Scikit-learn To be implemented
implied_cov Implied Covariance Risk Model Implied Covariance Matrix To be implemented
semi_cov Semi-covariance Risk Model Semi-Covariance Matrix semi_cov.py
ew_cov Exponentially-Weighted Covariance Risk Model EW Covariance Matrix ew_cov.py
cov_denoising Covariance Denoising Risk Model Covariance Denoising To be implemented
cov_detoning Covariance Detoning Risk Model Covariance Detoning To be implemented

II) Covariance Shrinkage

Model Tag Model Name Documentation Code
Covariance Shrinkage Risk Models
cov_shrinkage Covariance Shrinkage Risk Models RiskModels.md cov_shrinkage.py
cov_shrinkage.shrunk_covariance Covariance Shrinkage - Manual Shrinkage RiskModels.md cov_shrinkage.py
cov_shrinkage.ledoit_wolf Covariance Shrinkage - Ledoit-Wolf RiskModels.md cov_shrinkage.py
cov_shrinkage.oracle_approximating Covariance Shrinkage - Oracle Approximating RiskModels.md cov_shrinkage.py

III) Sparse Inverse Covariance Estimators

Model Tag Model Name Documentation Code
Sparse Inverse Graphical Lasso Covariance Estimator
graph_lasso_cov Sparse Inverse Graphical Lasso Covariance Estimator Scikit-learn To be implemented

IV) Robust Covariance Estimators

Model Tag Model Name Documentation Code
Robust Covariance Estimators
mcd_cov Robust Minimum Covariance Determinant (MCD) Estimator Scikit-learn To be implemented
gerber_cov Robust Gerber Statistic for Covariance Estimation The Gerber Statistic To be implemented

We can implement the aforementioned expected return models as detailed below. We can also plot the calculated covariance estimations and compare them with the real future covariance matrix, in order to observe which covariance estimator performs best:

  
    from pyfinpo.input_estimates import risk_models

    cov_matrix = risk_models.sample_cov(prices)
    po_plotting.plot_covariance(sample_cov, plot_correlation=True)
    plt.show()

Quick Example:

3.1.2

___ INPUT ESTIMATE 2

Expected

Return Models

Risk

Models

__ PYFINPO FEATURE II

3.2

Portfolio
Optimization

__ Portfolio Optimization I

3.2.1

PO Models

The Portfolio Optimization Model of choice will determine the strategy to follow in the rest of the portfolio optimization process. It dictates how we are approaching the PO problem.

__ Portfolio Optimization II

3.2.2

PO Objectives

The Portfolio Optimization Objectives will define the metric for which we want to optimize the portfolio allocation process. PyFinPo offers several options for risk/return metrics.

__ Portfolio Optimization IV

3.2.4

PO Period

Portfolio Optimization Period defines the Investment Horizon of choice for the optimization, and formulates the problem based on a discrete or continuous time approach.

__ Portfolio Optimization V

3.2.5

PO Solver

Finally, the last step of the Portfolio Optimization process defines the solver (optimizer) to address the actual optimization problem.

3.2

__ Portfolio Optimization III

3.2.3

PO Constraints

The Portfolio Optimization Constraints define the conditions and rules that will govern the Optimization problem.

I) Naive PO Models

Model Tag Model Name Documentation Code
eqw_po Equal Weight (1/N) Portfolio Optimization skfolio To be implemented
ivp_po Inverse Volatility Portfolio (IVP) Optimization skfolio To be implemented
random_po Random Portfolio Optimization (Dirichlet Distribution) skfolio To be implemented
Model Tag Model Name Documentation Code
mr_po Mean-Risk Portfolio Optimization (generalizes all models below) skfolio To be implemented
mv_po Mean-Variance Portfolio Optimization PyPortOpt mv_po.py
msv_po Mean-Semivariance Portfolio Optimization PyPortOpt msv_po.py
mcvar_po Mean-CVaR (Conditional Value at Risk) Portfolio Optimization PyPortOpt mcvar_po.py
mcdar_po Mean-CDaR (Conditional Drawdown at Risk) Portfolio Optimization PyPortOpt mcdar_po.py

List of Risk Measures Supported under MeanRiskPO class:

  • Mean Absolute Deviation

  • Variance (Second Central Moment)

  • Skewness (Normalized Third Central Moment)

  • Kurtosis (Normalized Fourth Central Moment minus 3)

  • Fourth Central Moment

  • First Lower Partial Moment

  • Semi-Variance (Second Lower Partial Moment)

  • Fourth Lower Partial Moment

  • Value at Risk

  • Maximum Drawdown

___ PORTFOLIO OPTIMIZATION I

Portfolio

Optimization Models

The first step of the portfolio optimization is to choose the optmization model/framework. The model of choice is going to determine the type of approach we want for the portfolio optimization, the different objective functions that we will be able to optimize for, and the solver used to approach the optimization problem, among other things. As we will see later on, each optimization model/framework has its particular objective functions and solvers/optimizers.

The following Portfolio Optimization Models have been/will be implemented:

___ PORTFOLIO OPTIMIZATION II

Portfolio

  • Average Drawdown

  • Drawdown at Risk

  • Entropic Risk Measure

  • CVaR (Conditional Value at Risk)

  • EVaR (Entropic Value at Risk)

  • CDaR (Conditional Drawdown at Risk)

  • EDaR (Entropic Drawdown at Risk)

  • Worst Realization

  • Ulcer Index

  • Gini Mean Difference

Optimization Objectives

Figure 2 - Mean-Variance Efficient Frontier. Source: PyPortOpt

I) Objective Functions

Some of the Portfolio Optimization Models exposed above are self-descriptive, in the sense that by definition they only posses a single possible objective function to optimize. In these cases, the default objective function will be automatically chosen by the code implementation, and the user will not need to specify any objective.

However, there are other models (the most obvious kind being Mean-Risk models) which allow to select different objective functions to optimize for. The easiest way to picture this behavior is with Mean-Variance theory as an example (see Figure 2). Within the MVT framework we can define the Efficient Frontier, which represents a Pareto Optimal set of possible optimal portfolios.For a given Efficient Frontier, different points can be selected as optimal under different objective functions.

In this context, PyFinPO provides five main objective functions:

  • Minimum Risk - global_min_risk

    • Represents the point of the Optimal Set with lowest level of risk. Its calculation can be useful to have an idea of how low risk could be for a given problem/portfolio.

  • Minimize Risk - min_risk

    • Minimizes risk for a given level of return.

  • Maximize Return - max_return

    • Minimizes return for a given level of risk.

  • Maximize Ratio - max_ratio

    • Maximizes the ratio return-risk for the whole portfolio. This returns the tangency portfolio, as it represents the point on a returns-risk graph where the tangent to the efficient frontier intersects the y-axis at the risk-free rate. This is the default choice as it finds the optimal return per level of risk at portfolio level.

  • Maximize Utility - max_return

    • Maximizes the utility function provided manually by the user, which specifies its level of risk aversion.

Once again, the word "risk" can be replaced for any of the available risk metrics defined under MeanRiskPO class (see list above).

Note: not all of these objective functions may be available for all the different Mean-Risk models.

II) Adding Custom Objectives

In addition, sometimes we may want to add extra optimization objectives that are not defined in the previous 5 objective functions.

PyFinPO supports the addition of extra optimization objectives. Note that there are 2 types of objectives, convex and non-convex. While convex objectives fit nicely under a convex optimization solver, non-convex objectives may be treated with care as they may produce incompatibilities with the solvers implemented in this library.

  • Convex Objectives:

    • L2 regularisation (minimising this reduces nonzero weights)

    • Transaction cost model (can be added also as constraint)

    • Custom convex objectives (must be expressed with cvxpy atomic functions)

  • Non-Convex Objectives:

    • See example in the original docs of the PyPortOpt library here


For an example on how to implement custom objectives, see PyFinPO-UserGuide.

III) Single-Objective vs Multi-Objective Optimization

Note that when we provide an specific objective function or set of objectives for the portfolio optimization, it will return a single solution (i.e. single set of optimal weights that represent the optimal portfolio).

Alternatively, we can change our approach and implement a multi-objective optimization where we obtain an optimal set of solutions from which we can choose the preferred one for our objectives. A way to do this, is by plotting the optimal set of solutions (e.g. efficient frontier in case of Mean-Variance Theory) and then choosing the desired portfolio.

___ PORTFOLIO OPTIMIZATION III

Portfolio

Optimization Constraints

3.2.1

Constraints and objectives are treated similarly from an optimization point of view. Therefore, the methodology to add constraints to a portfolio optimization is almost equivalent to the process of adding objectives described above.

The main portfolio optimization constraints available in PyFinPO are:

  • Market Neutrality

  • Long/Short Portfolio

  • Weight Bounds (limit the position size of securities)

  • Sector & Security Constraints

  • Score Constraints

  • Nº of Asset Constraints (Convexity Constraints)

  • Tracking Error Constraints

For examples on how to implement custom objectives in PyFinPO, see PyFinPO-UserGuide.

II) Risk-Based PO Models

Model Tag Model Name Documentation Code
gmv_po Global Minimum Variance PO PyPortOpt, GMVP To be implemented
maxdiv_po Maximum Diversification Portfolio Optimization skfolio To be implemented
risk_parity_po Risk Parity Portfolio Optimization skfolio, Risk Parity PO To be implemented
risk_budgeting_po Risk Budgeting Portfolio Optimization skfolio, Risk Budgeting PO To be implemented

III) Mean-Risk PO Models

Mean-Risk Portfolio Optimization models aim to find asset combinations which optimize the relationship return vs risk. The most well-known Mean-Risk model is Mean-Variance Portfolio Optimization, which uses the variance of asset returns as measure of risk. However, many different measures of risk can be selected, giving rise to a wide range of Mean-Risk models.

PyFinPO provides direct implementation of the most relevant Mean-Risk models, as detailed in the summary table below (Mean-Variance, Mean-Semivariance, Mean-CVaR, Mean-CDaR). In order to select any other measure of risk which is not directly implemented in the PO models below, the parent class MeanRiskPO generalizes all mean-risk models and allows to choose among any of the available risk metrics:

IV) Robust Mean-Risk PO Models

V) Clustering PO Models

Model Tag Model Name Documentation Code
cla_po Critical Line Algorithm (CLA) Portfolio Optimization PyPortOpt cla_po.py
dr_cvar_po Distributionally Robust CVaR Portfolio Optimization skfolio To be implemented
Model Tag Model Name Documentation Code
hrp_po Hierarchical Risk Parity (HRP) Portfolio Optimization mlfinlab hrp_po.py
herc_po Hierarchical Equal Risk Contribution (HERC) Portfolio Optimization mlfinlab To be implemented
nco_po Nested Clustered Optimization (NCO) mlfinlab To be implemented

VI) Ensemble PO Models

Model Tag Model Name Documentation Code
stack_po Stacking Portfolio Optimization - To be implemented

___ PORTFOLIO OPTIMIZATION IV

Portfolio

Optimization Period

One of the main limitations of PyFinPO and most other Portfolio Optimization libraries is that the optimization is static (single-period), meaning that based on the input parameters the output optimal portfolio is only valid for a static period of time. Of course, due to the dynamic nature of financial markets it would be preferable to have a dynamic optimization in order to reflect the latest information available in the optimized portfolio and take optimal rebalancing decisions.

Future development plans for PyFinPO include extending the optimization functionalities to address the portfolio optimization problem dynamically. Two main approaches can be found in literature that address PO dynamically, as a Multi-Period Portfolio Optimization (MPPO):

  • The first approach considers a discrete-time PO, where the expected utility of the investor terminal wealth is maximized over a multi-period investment horizon, and portfolio can be rebalanced only at discrete points in time (e.g. for a 1-year PSP, adjusting portfolio weights at the beginning of every month).

  • The second approach is a continuous-time optimization, where asset weights can be reallocated at any time within the investment horizon.

Zhang et. al. provide a detailed review on the formulation and advantages of dynamic PO techniques.

___ PORTFOLIO OPTIMIZATION V

Portfolio

3.2.3

3.2.4

3.2.5

Optimization Solver (Optimizer)

3.2.2

The solver implemented to address the optimization problem in the previous examples has been implemented under the hood of the MeanVariancePO class, which inherits its methods from the BaseConvexOptimizer class. In the context of Mean-Variance theory, as the optimization problem is typically convex (unless non-convex constraints or objectives are introduced), it can be solved via quadratic programming with the cvxpy python library for convex optimization.

While Mean-Variance optimization framework can be addressed with convex optimization, other portfolio optimization models which are completely different in character may use different optimization schemes. An overall summary is presented below for quick reference, including only the main portfolio optimization models and the optimization solver they use in this library.

Portfolio Optimization Model Module Main Class Optimization Solver Optimization Solver Details
Mean-Variance Portfolio Optimization mv_po.py MeanVariancePO BaseConvexOptimizer MVPO is addressed with convex optimization via cvxpy
Mean-SemiVariance Portfolio Optimization msv_po.py MeanSemivariancePO BaseConvexOptimizer MSVPO can be re-written as convex problem (full details here)
Mean-CVaR Portfolio Optimization mcvar_po.py MeanCVaRPO BaseConvexOptimizer MCVaRPO can be reduced to linear program (full details here)
Mean-CDaR Portfolio Optimization mcdar_po.py MeanCDaRPO BaseConvexOptimizer MCDaRPO can be reduced to linear program (full details here)
Critical Line Algorithm Portfolio Optimization cla_po.py CLAPO BaseOptimizer CLAPO uses CLA convex optimization solver, specifically designed for PO
Hierarchical Risk Parity Portfolio Optimization hrp_po.py HRPPO BaseOptimizer HRPPO implements hierarchical clustering optimization (more details here)

*For a more detailed analysis on how to choose the right solver for any risk metric, visit Riskfolio-Lib - Choosing a Solver.

__ PYFINPO FEATURE III

3.3

Portfolio Performance

The Portfolio Performance module is a key component of the portfolio optimization repository, designed to evaluate and analyze the effectiveness of optimized portfolios. It is in charge of computing essential performance metrics such as expected annual return, volatility (risk), and Sharpe Ratio, providing a comprehensive view of portfolio performance. These metrics help investors assess the trade-off between risk and return, ensuring that the portfolio aligns with their investment goals. By leveraging this module, users can make data-driven decisions and refine their strategies for better financial outcomes. The module is flexible, easy to integrate, and supports various portfolio optimization models.

3.3

__ PYFINPO FEATURE III

3.4

Portfolio
Post-Processing

__ Post-Processing I

3.4.1

Portfolio
(Tidy) Weights

Express portfolio optimal weights in a more visual, tidy way.

__ Post-Processing II

3.4.2

Portfolio
Discrete Allocation

Express portfolio weights in execution terms (how much quantity of each stock to buy at the current market price).

3.4

___ PORTFOLIO POST-PROCESSING I

Portfolio

3.4.1 

  
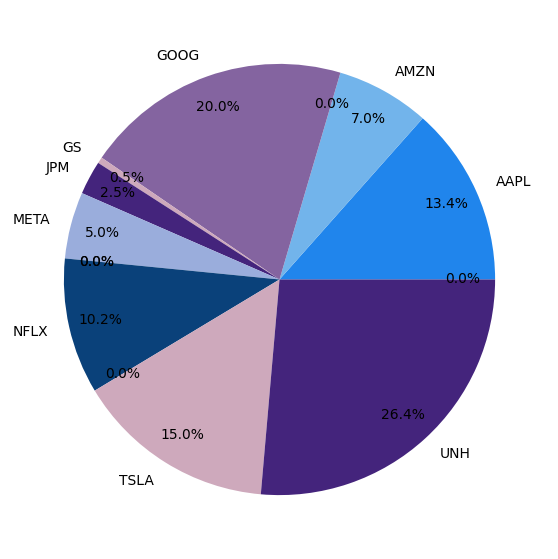
    mv_po = po_models.MeanVariancePO(mhr, sample_cov, weight_bounds=(0,1))

    mv_po.min_volatility()
    optimal_portfolio_clean_weights = mv_po.clean_weights()
    optimal_portfolio_clean_weights
  

  
  pd.Series(mv_po).plot.pie(figsize=(7,7), colors=colors, autopct='%1.1f%%', pctdistance=0.85)

(Tidy) Weights

PyFinPo also offers the option to express portfolio optimal weights in a more visual, tidy way with the .clean_weights() method (see PyFinPO-UserGuide).

___ PORTFOLIO POST-PROCESSING II

Portfolio

3.4.2

Discrete Allocation

Once we have the optimal portfolio weights, it is probably useful to express it in execution terms (how much quantity of each stock to buy at the current market price). The function discrete_allocation helps us with this purpose:

  
    from pyfinpo.utils import DiscreteAllocation

    latest_prices = prices.iloc[-1]  # prices as of the day you are allocating
    da = DiscreteAllocation(optimal_portfolio_weights, latest_prices, 
                            total_portfolio_value=20000, short_ratio=0.3)
    alloc, leftover = da.lp_portfolio()
    print(f"Discrete allocation performed with ${leftover:.2f} leftover")
    {key: float(value) for key, value in alloc.items()}
  

  
    #Output:

    
    Discrete allocation performed with $13.46 leftover
    {'AAPL': 3.0,
     'GOOG': 8.0,
     'META': 5.0,
     'MSFT': 3.0,
     'PFE': 218.0,
     'TSLA': 2.0,
     'UNH': 4.0,
     'XOM': 46.0}

04

Future Works/Resources __________

Future Works & Resources

Chapter 4 -

3.3

Future

Works

Some of the improvements that may be added in future versions of PyFinPO include the following:

  • Develop detailed documentation for models and API usage under docs folder.

  • Finish implementation of all the return models, risk models and portfolio optimization models whose status appears as "To be implemented" in the summary tables described above.

  • Include the implementation of multi-period optimization. See more details in Section 3.2.4.

  • Improve Portfolio Performance function to depict a more detailed analysis about the optimized portfolio, including additional measures of risk, performance ratios, backtesting functionalities, sensitivity analysis...

  • Implement tests for all library functionalities under the folder tests.

  • Add additional tutorials under the folder tutorials (currently only 2 are available) to cover more practical use cases of different optimizations and functionalities that can be performed with PyFinPO.

Source

Libraries

PyFinPO is an abstraction built on top of the following Python libraries:

Portfolio

SEE MORE PROJECTS

MATH, PHYSICS & ENGINEERING PROJECTS

COMPUTER SCIENCE PROJECTS

ML & AI PROJECTS

QUANT FINANCE PROJECTS

Next

Project Two