Optimization of Lunar Trajectories & Rendezvous Strategies in the Vicinity of the Moon
PROJECTS · MATH, PHYSICS & ENGINEERING
Math, Astrophysics
600h
Jan. 2018 - Aug. 2018
INTRO
Project Description
The objective of this project in collaboration with the German Aerospace Center (DLR) and the University ISAE-SUPAERO, is to find the optimal trajectories between the surface of the Moon and the Near-Rectilinear Halo Orbits (NRHO), where a new Lunar Orbital Platform-Gateway (LOP-G) is to be placed, as proposed by DLR studies.
To achieve this goal, a comparative case-study analysis has been performed between some of the principal parameters that constitute the optimal control problem that will govern the dynamics of the mission (i.e. coordinate systems, optimization techniques, transcription laws…). Several optimizations have thus been performed across different one-phase and two-phase mission scenarios in the Python package OpenMDAO, with the objective to find the best configurations to calculate optimal lunar trajectories.
SKILLS
Fields of Expertise
Research:
Math/Physics:
Optimization:
Coding (Python):
Scientific Writing:
Complexity: ★★★★☆
Tools: Python, Optimal Control
Project Type: MSc. Thesis
ABOUT
Abstract
A new transportation system is being studied at DLR, which proposes the implementation of a Lunar Orbital Platform-Gateway (LOP-G) in a Near Rectilinear Halo Orbit (NHRO) in the vicinity of the Moon, to act as cargo station to decrease fuel consumption of lunar operations. The objective of the present project is to find the optimal trajectories between the surface of the Moon and the RHO, where the LOP-G is to be placed. To achieve this goal, a comparative case-study analysis has been performed between some of the principal parameters that make up an optimal control problem (i.e. coordinate systems, optimization techniques and transcription laws). Several optimizations have been hence performed across different one and two-phase mission scenarios in the python package OpenMDAO, with the objective to find the best configurations to calculate the optimal lunar trajectories.
The case-study comparison between coordinate systems (polar, spherical and Cartesian) has determined that polar coordinates are ideal as first implementation, offering up to 30% higher convergence rates and 50% less time of convergence than their counterparts for two-dimensional optimization problems. Conversely, spherical coordinates present the most accuracy of results for transfers in the three-dimensional space. In terms of optimization techniques, shooting methods have demonstrated 20% to 40% increases in convergence rates and less dependency on the initial guess as compared to collocation points, which in turn offer more precise results for optimizations (usually less than 5-10% error). Analysis of transcription laws have shown that Gauss-Lobatto collocation points presented up to 20% higher velocity of convergence than Radau pseudospectral collocation methods, and between 5% and 10% improvements in convergence rates.
From this results, it was inferred that polar coordinates and collocation points with Gauss-Lobatto transcription methods were most suitable for our purposes, and consequently used to calculate the optimal trajectories.
Ascending trajectories from lunar surface to Low Lunar Orbit (LLO) were calculated in the first place, obtaining a Time of Flight (TOF) of 3572s and a final to initial Mass Ratio (MR) of 0.67 for the one-phase trajectory, and a TOF of 3443s and MR of 0.62 for the two-phase trajectory. The lunar descent trajectories from LLO to Moon surface were computed in the second place, obtaining a TOF of 4431s and MR of 0.76 for the one-phase trajectory and a TOF of 4377s and MR of 0.72 for the two-phase trajectory. Finally, the rendezvous trajectory between LLO and NRHO was optimized using a shooting method as initial guess to facilitate convergence, and a Gauss-Lobatto collocation method to obtain highest precision for the final results. The optimization offered low convergence rates (around 10%) but relatively good precision of trajectory results (less than 5-10% error), in comparison to optimized results by external sources using convex optimization methods.
Project Tags:
Astrodynamics
Space Mission Design
Orbit Determination
Three-Body Problem
Space Rendezvous
Space Trajectory Optimization
0
INTRODUCTION
CHAPTER
___ INTRO
Problem Context
In the context of space exploration, the Moon is for the spatial community a promising focus point as a preliminary step for future access to further areas of the solar system. Up to now, extensive experience exists regarding lunar trajectories and the execution of rendezvous operations in Earth and lunar environments. However, in order to make human presence in the moon sustainable, the nature of future spatial missions requires a new approach.
One of the main challenges of making lunar missions sustainable in the long term, is their dependency on time and fuel efficiency. In this context, it is believed to be much more beneficial to develop new operations in the vicinity of the Earth-Moon Lagrangian (EML)1 points, due to the fuel optimization advantages that may present. However, despite these potential benefits relatively few missions have been attempted under such circumstances, due to the fact that classical Keplerian dynamics no longer apply in these conditions, among other factors.
To provide a solution to this question, the DLR2 in collaboration with ISAE-Supaero, is studying the implementation of a Lunar Orbital Platform-Gateway (LOP-G), along with a new transportation system to perform rendezvous missions in the vicinity of the Earth-Moon Lagrangian point. The aim of the LOP-G is to act as a mid-way station for fuel and cargo exchange between Earth and Moon, decreasing fuel consumption levels and serving as a lunar gateway for further exploration of the solar system.
DLR has identified two main steps in the design process of the new Moon transportation system: the mission design strategy and the optimization of the lunar orbital trajectories. Previous mission analysis [5, 13] have demonstrated that the optimal design strategy for such kind of mission includes trajectories between Low Earth Orbits (LEO), Low Lunar Orbits (LLO) and the Moon surface, with an intermediate staging orbit located in the vicinity of the EML. With the mission design strategy already defined, the main challenge that remains to be addressed is the optimization of the spatial trajectories between orbits.
___ INTRO
Research Scope & Objectives
The present investigation takes place under DLR’s project of designing a new transportation system in cis-lunar environment (i.e. between Moon and Earth), in order to achieve sustainable human presence in the the Moon, as intermediate step to further exploration of the solar system.
In this context, with the main sections of the mission design completely determined, the scope of the present project will focus on the optimization of lunar trajectories between Moon, Earth and the LOP-G, located in a staging orbit in the vicinity of EML points. More specifically, Near Rectilinear Halo Orbits3 are believed to be the ideal staging orbit for the LOP-G and the purposes of the mission.
Under these circumstances, it is possible to divide the problem into two different phases: the initial phase addresses the optimization of lunar ascending and descending trajectories from Moon surface to LLO, and the second phase comprises the optimization of rendezvous strategies between LLO and NRHO. Out of the scope of the project will remain the optimization of trajectories from LEO to NRHO.
The main objective of the present project concerns the study and comparison of the most relevant lunar trajectory optimization parameters, in order to find the optimal trajectories between lunar surface and NRHO. Due to the constraints of the investigation, the present project will focus solely on some of the most relevant trajectory optimization parameters for the purposes of DLR’s mission, and by no means pretends to be an exhaustive comparison of all the existing optimization techniques. More specifically, and in order to accomplish the principal objective of the investigation, the project aims to complete the following sub-objectives:
More specifically, and in order to accomplish the principal objective of the investigation, the project aims to complete the following sub-objectives:
Comparison of lunar ascending and descending trajectory optimization performance for polar, spherical and Cartesian coordinate systems.
Comparison of lunar ascending and descending trajectory optimization performance for different optimization techniques: orthogonal collocation, pseudospectral methods and shooting methods.
Comparison of lunar ascending and descending trajectory optimization performance for different transcription methods: Gauss-Lobato and Radau.
Comparison of lunar trajectory optimization for different ascending and descending mission constraints: one/two phase trajectories, vertical/unconstrained rise (or powered descent).
Based on the previous results, determine the best approach for the optimization of rendezvous strategies between LLO and NRHO.
In order to accomplish these objectives, it will be necessary to first introduce a succinct review of the state of the art, along with the mathematical methods, the formulation of the optimal control problems and the methodology to perform the optimizations.
1
RESEARCH
CHAPTER
__ STATE OF THE ART
Literature Review
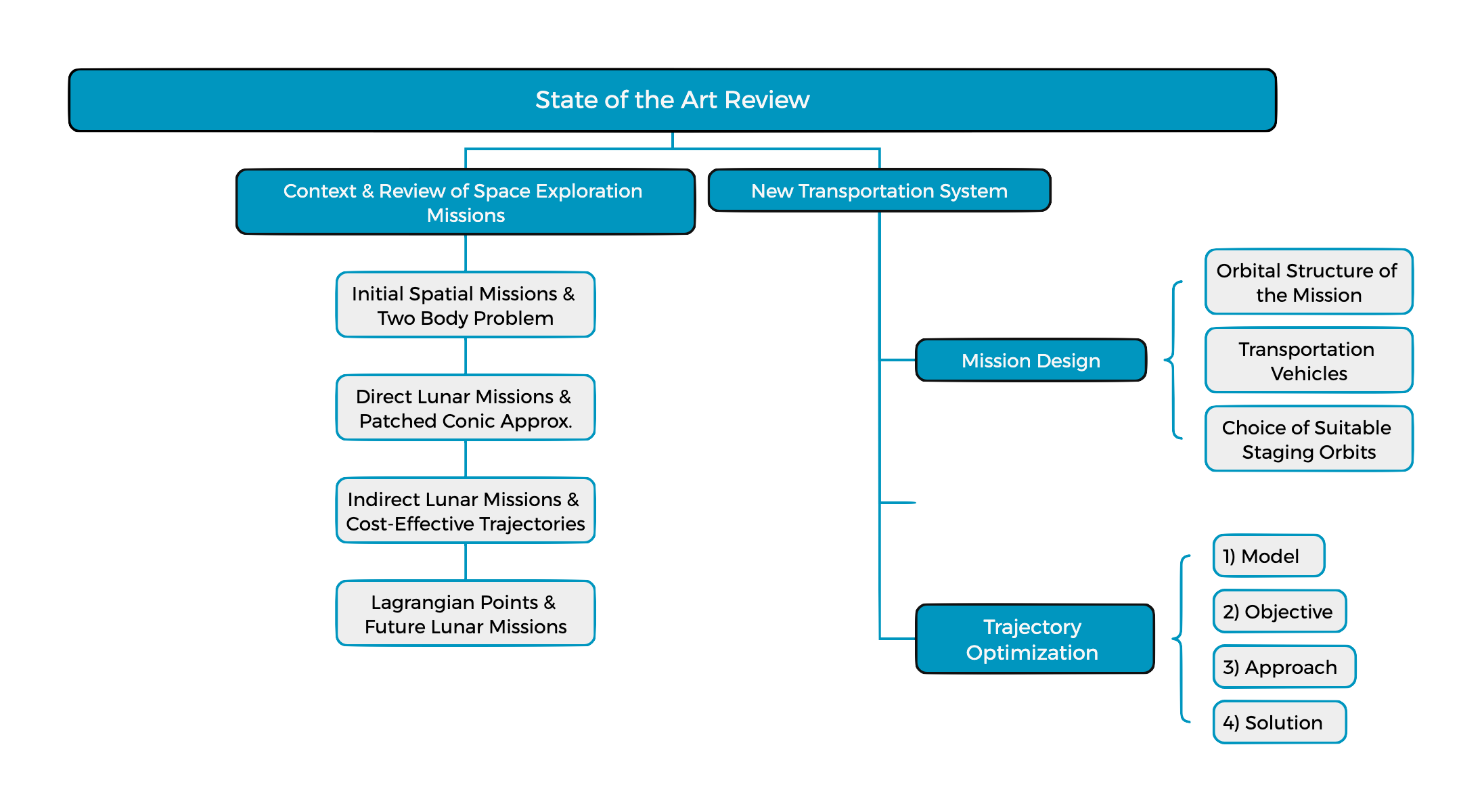
With the objective to provide further scientific background and to understand the foundations of the new lunar transportation system, the present section aims to describe the most relevant investigation methods and state of the art review on lunar mission design and optimization strategies.
2
Mathematical Models
CHAPTER
__ MATHEMATICAL MODELS
Trajectory Dynamics & Optimization
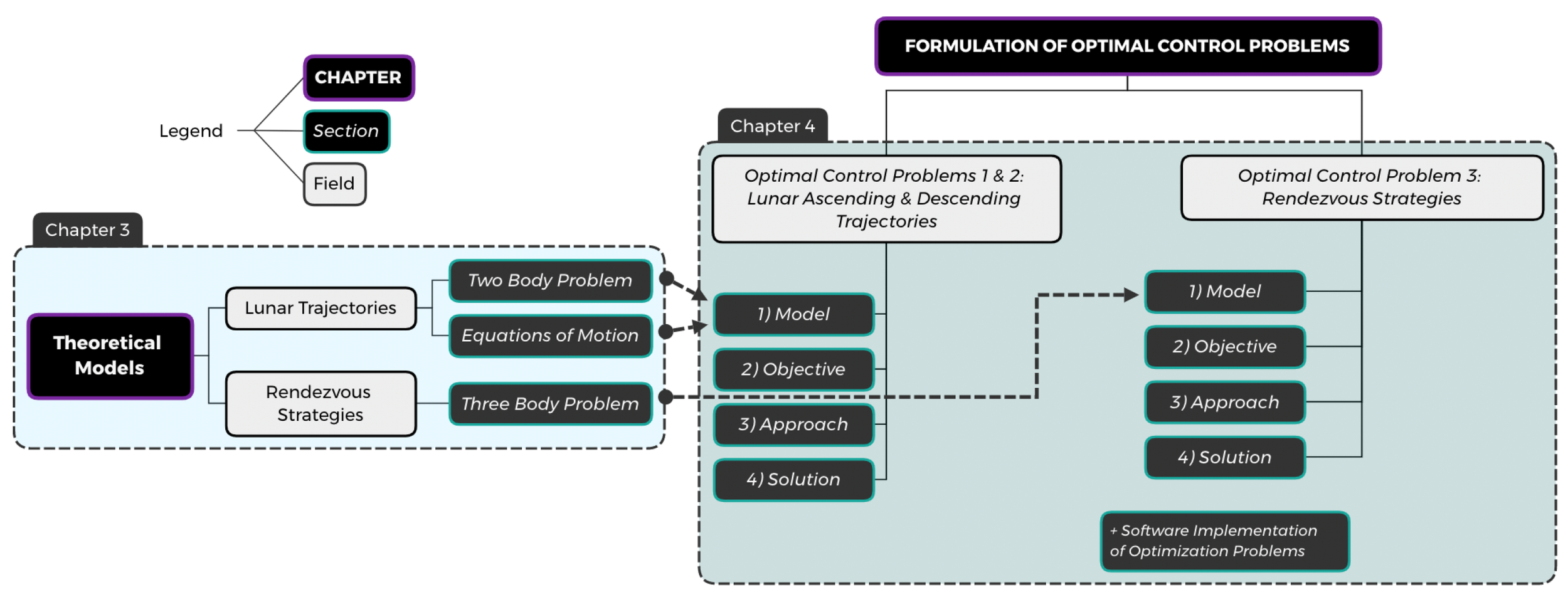
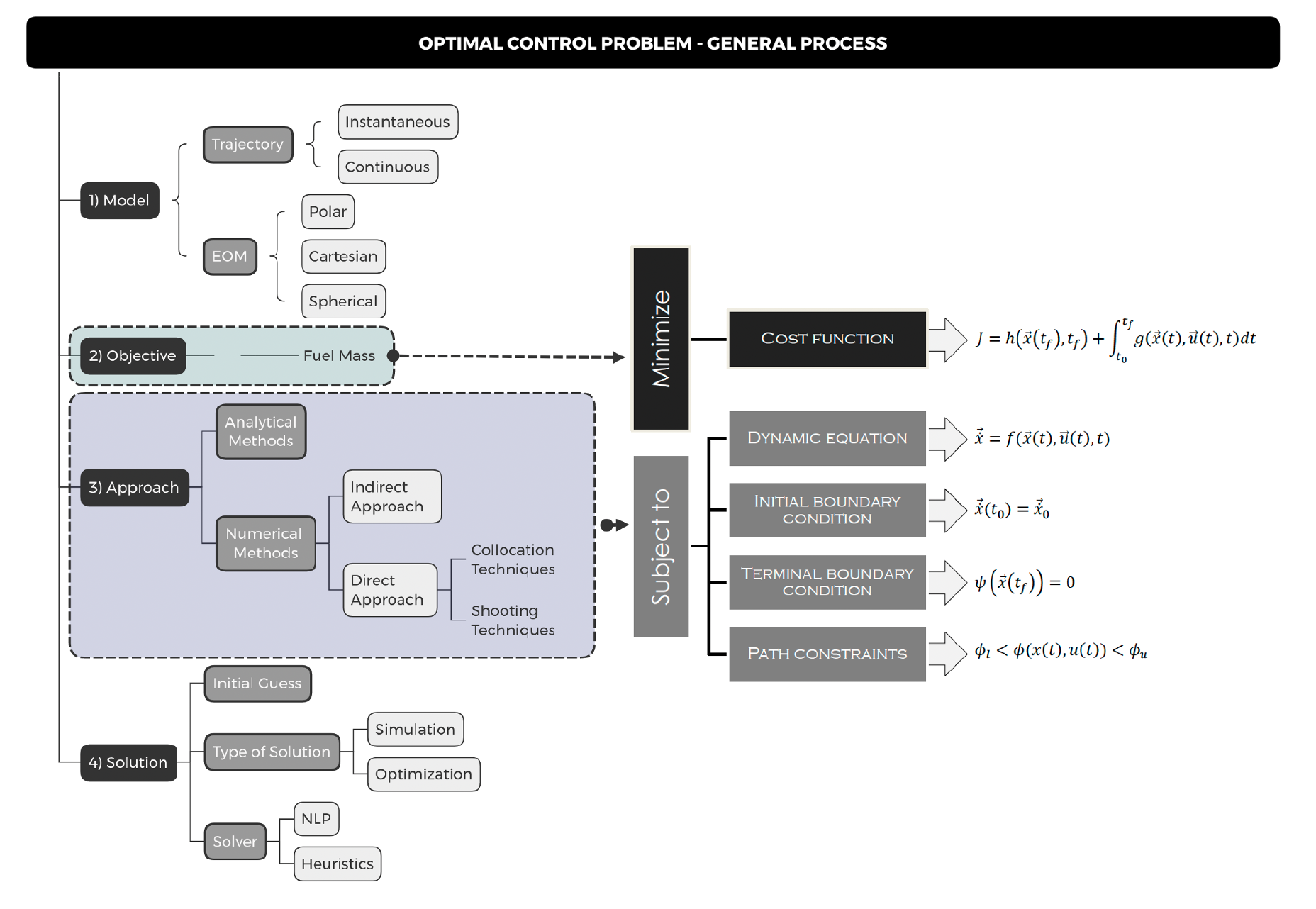
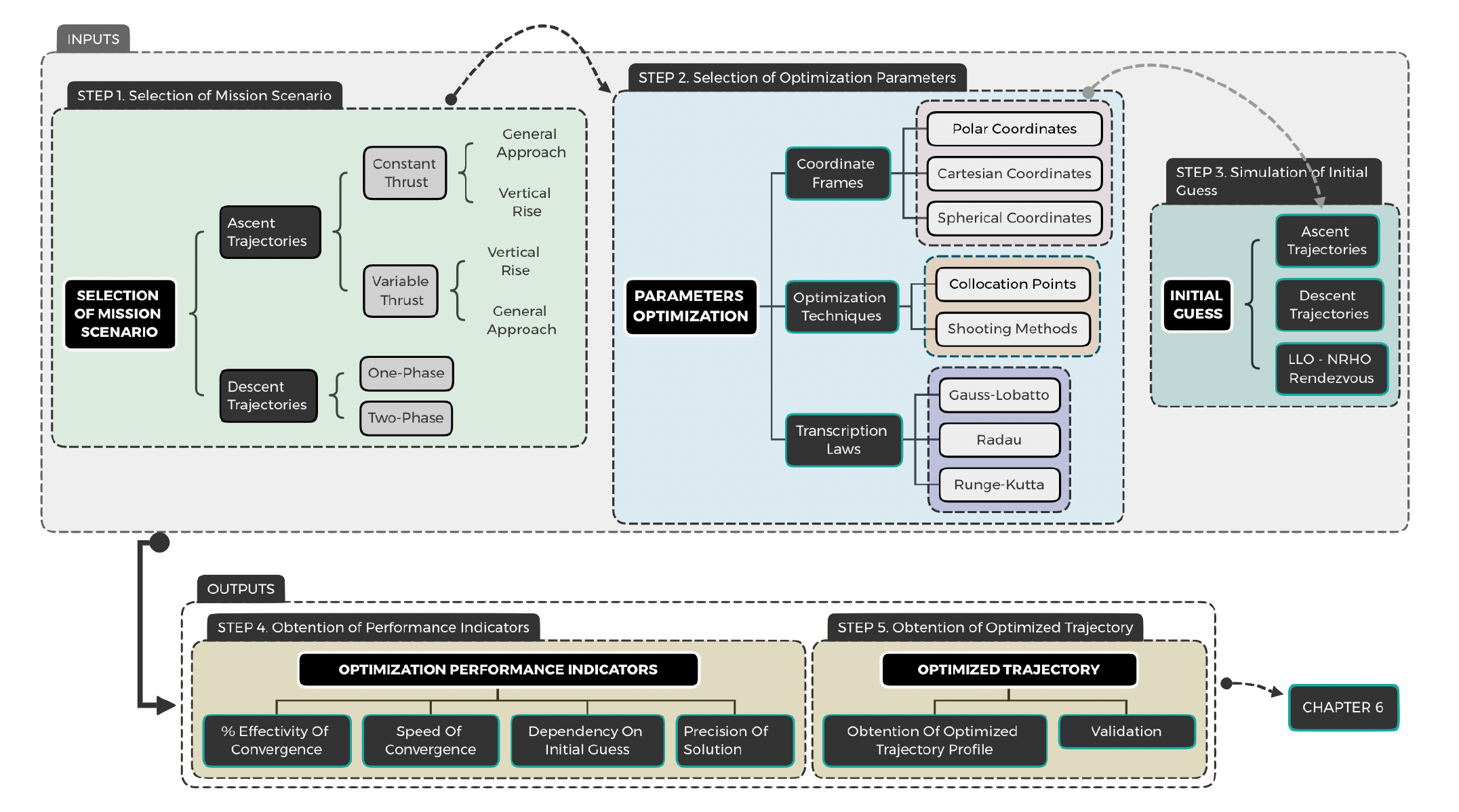
The objective of this chapter is to cover in a succinct way the main theoretical concepts that will lay the foundations for the present investigation. As previously defined in Figure 2.13, any optimization problem can be divided in 4 steps. This chapter aims to define the first step of the optimization problem—the mathematical models —for the three types of optimization problems (OCP) that comprise the present project: the lunar trajectory optimization problem (OCP1 and OCP2), and the rendezvous optimization problem (OCP3). Upon definition of the models theoretical background, chapter 3 will define the Optimal Control Problems of study.
___ PROBLEM DYNAMICS
The objective of this chapter is to formulate the Trajectory Optimization Problems that correspond to the two phases of the project: the lunar ascending and descending trajectories from Moon surface to LLO, and the rendezvous operations from LLO to NRHO.
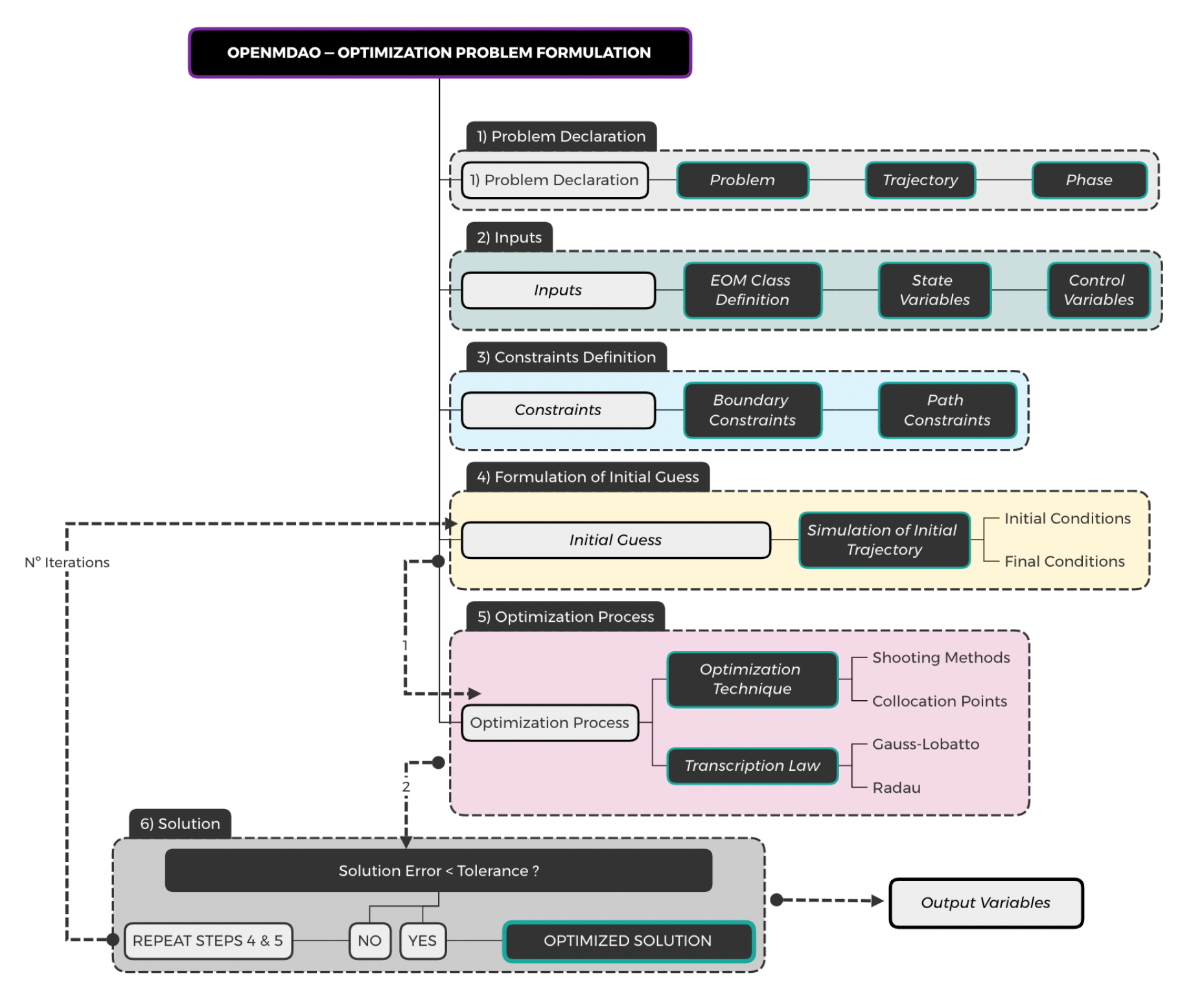
Figure 4.2 provides the general scheme of the optimization process, organized according to the 4-steps and the different optimization parameters that they present. This general approach comprises the formulation of the mathematical model of the problem, the definition of the principal objectives, the development of a suitable approach to reach those objectives, and the process to achieve the solution of the optimal problem (approached with library OPENDMAO).
2.2) Optimal Control Problem
2.1) Theoretical Models
___ TRAJECTORY OPTIMIZATION
-
Equations of Motion of 2 bodies in the space (Two-Body problem)
Conservation of Energy and Angular Momentum
Orbit Equations and Conic Trajectories:
Elliptical Orbits
Hyperbolic Orbits
Determination of Orbital Position over Time
Perturbations
Planetary Propagators and Ephemerides
-
Based on the established 2BP framework, the next important mission is to provide the mathematical formulation for the problem. Depending on the objectives of the mission and the trajectories of interest, several approaches can be followed here to characterize the problem and adapt it to our circumstances, in order to describe the movement of the Lunar Module. Kelly [67] and Vinh et al. [15] present a good overall review of the most used coordinate frames for lunar missions, including cartesian, spherical, elliptical and Keplerian frames.
-
After the initial review of the Two Body Problem and the Equations of Motion relative to the lunar trajectories, the mathematical model has been set for the first two optimization problems, regarding the optimization of lunar ascending and descending trajectories. This section aims to provide the same theoretical background for the last optimization problem, relative to the optimization of the rendezvous operations between LLO and NRHO.
As compared to lunar trajectories, rendezvous missions in the vicinity of Lagrangian points are based on the 3BP hypothesis, where Keplerian dynamics no longer apply. The theoretical review of the circular restricted three body problem has been developed following the book by Koon et al. [47], which along with the articles [68] and [69], sets the basis for the three-body problem theory. The structure to be followed is depicted in Figure 3.5.
3
Results
CHAPTER
__ RESULTS
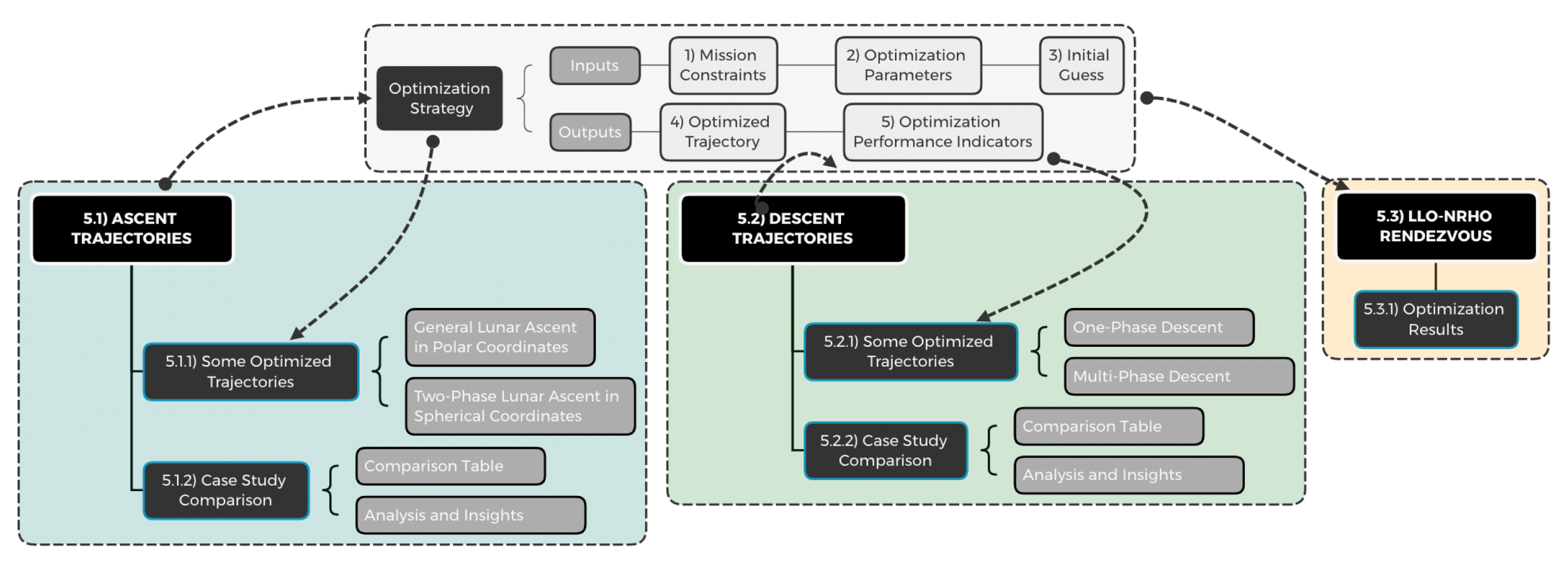
3.1) Case-Study Methodology
One of the objectives of this project is the presentation of the case-study comparison for the different optimization configurations. The structure of the case-study comparison procedure is detailed in the Figure below.
In the first place, the inputs are defined. The different mission scenarios were defined, in order to determine the objectives and details of the mission. Next, the optimization problem was defined according to the 4-step approach defined in past chapters. Next, the different optimization parameters (i.e. coordinate frames, optimization techniques and transcription laws) were compared. Finally, once the optimization problem was completely formulated, the outputs were determined. The optimization performance indicators that measure the quality of the optimization will be presented at the end of the present chapter, together with the optimization results for each mission and configuration type.
__ RESULTS
3.2) Results & Analysis
Figure below exhibits the process followed to obtain the optimization results, applying the optimization strategy process described in 5.1 to the ascent, descent and rendezvous trajectories. The process can be divided in 3 main stages: i) Optimization of Ascent Trajectories, ii) Optimization of Descent Trajectories, and iii) Optimization of LLO-NRHO Rendezvous.
. . .
I) Lunar Ascending Trajectory
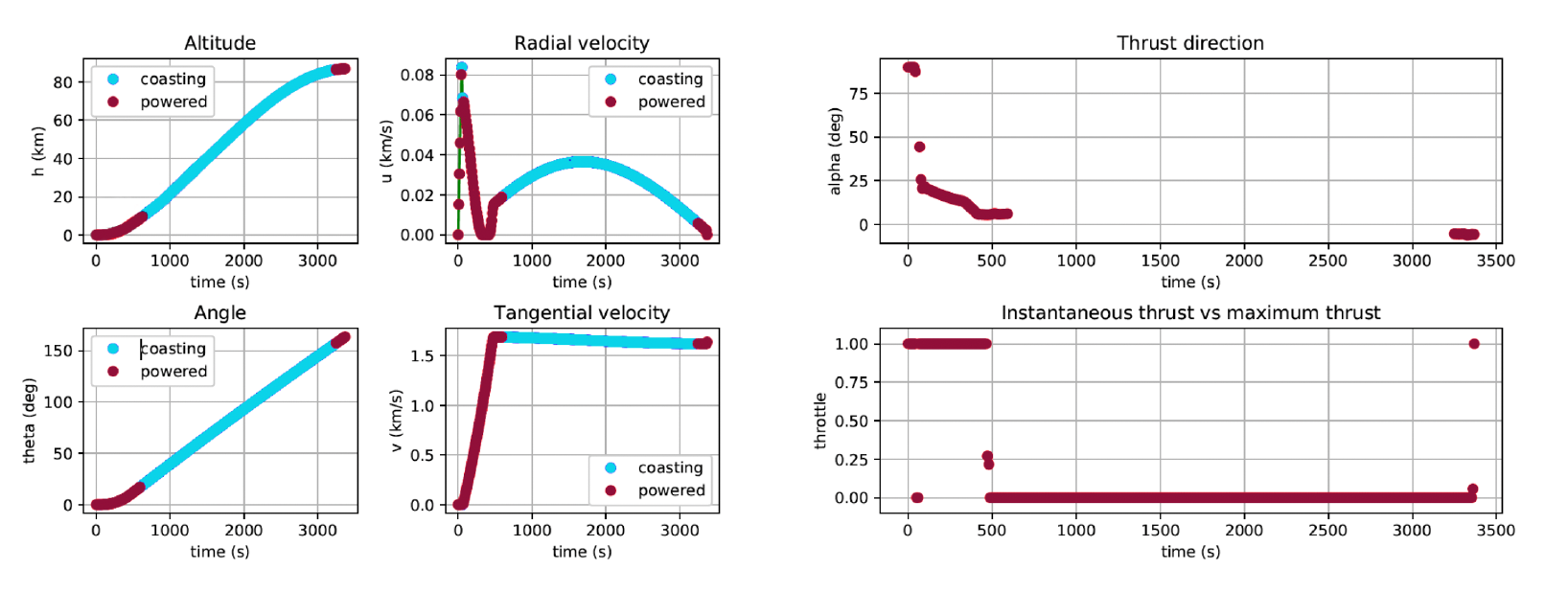
The general lunar ascent mission scenario was formulated in OCP1, and due to the simplicity of the polar coordinates, it is the perfect scenario to introduce the results for trajectory optimization.
Let us begin supposing that the objective of the mission is to calculate the optimized trajectory between a point located in the Moon’s surface (equatorial plane), and a circular LLO of H = 100 km altitude, also located in the equatorial plane (to avoid change of planes in the polar implementation).
The steps to follow for the optimization are the ones described in the Optimal Control Problem 1 in the right-hand side. In this case a Gauss-Lobatto transcription law with a third-order interpolating polynomial has been used to turn the continuous-time optimal control problem into the corresponding NLP problem, solved with the SNOPT routine.
The problem setup and the EOM class definition are introduced in the python optimizer OpenMDAO, and the interpolation points for the Hohmann initial guess are included. For the optimization parameters detailed in OCP1, the optimized trajectory is depicted in the figure below.
Section 6.1 addresses the problem of lunar ascending trajectories, applying the optimization strategy described in chapter 5 and then showing the results for the optimization. Section 6.2 details exactly the same procedure, applied for the descending lunar trajectories. Finally, section 6.3 covers the results relative to the optimization of the rendezvous operation between Low Lunar Orbit (LLO) and Near Rectilinear Halo Orbit (NRHO).
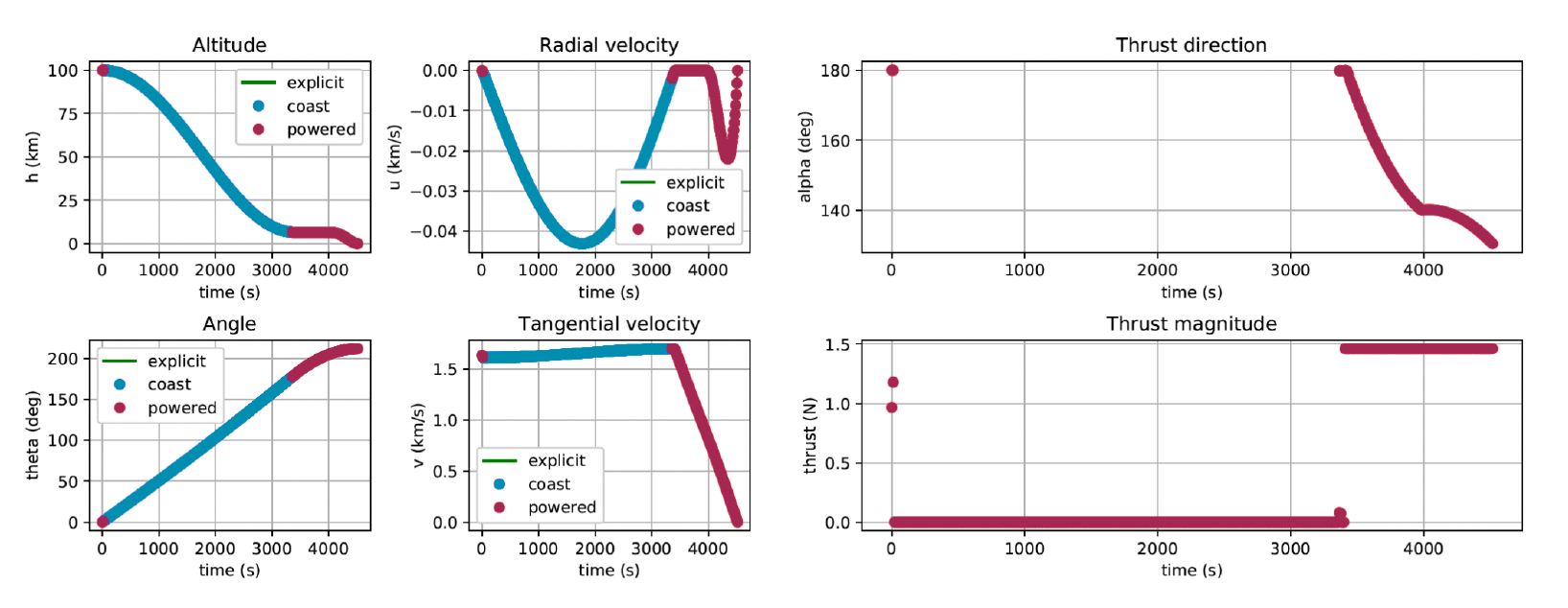
II) Lunar Descending Trajectory
The procedure to be followed in this section will be identical to the followed for the ascent trajectories. The general lunar descent is formulated in OCP3, and considers a one-phase descent with constant thrust.
We will compare the general descent with a second mission where descent trajectory will be divided in three different sections: first, a de-orbit burn to leave LLO orbit, followed by a Hohmann transfer from LLO to a lower periapsis altitude, from which the optimization trajectory will be performed to reach the ground. This strategy was similar to the one performed during the lunar missions of the program Apollo. Following the same steps as before, it is possible to formulate the optimization trajectory, from the 16km periapsis point to lunar surface.
The problem setup and the EOM class definition are introduced in the python optimizer OpenMDAO, and the interpolation points for the Hohmann initial guess are included. For the optimization parameters detailed in OCP1, the optimized trajectory is depicted in the figure below.
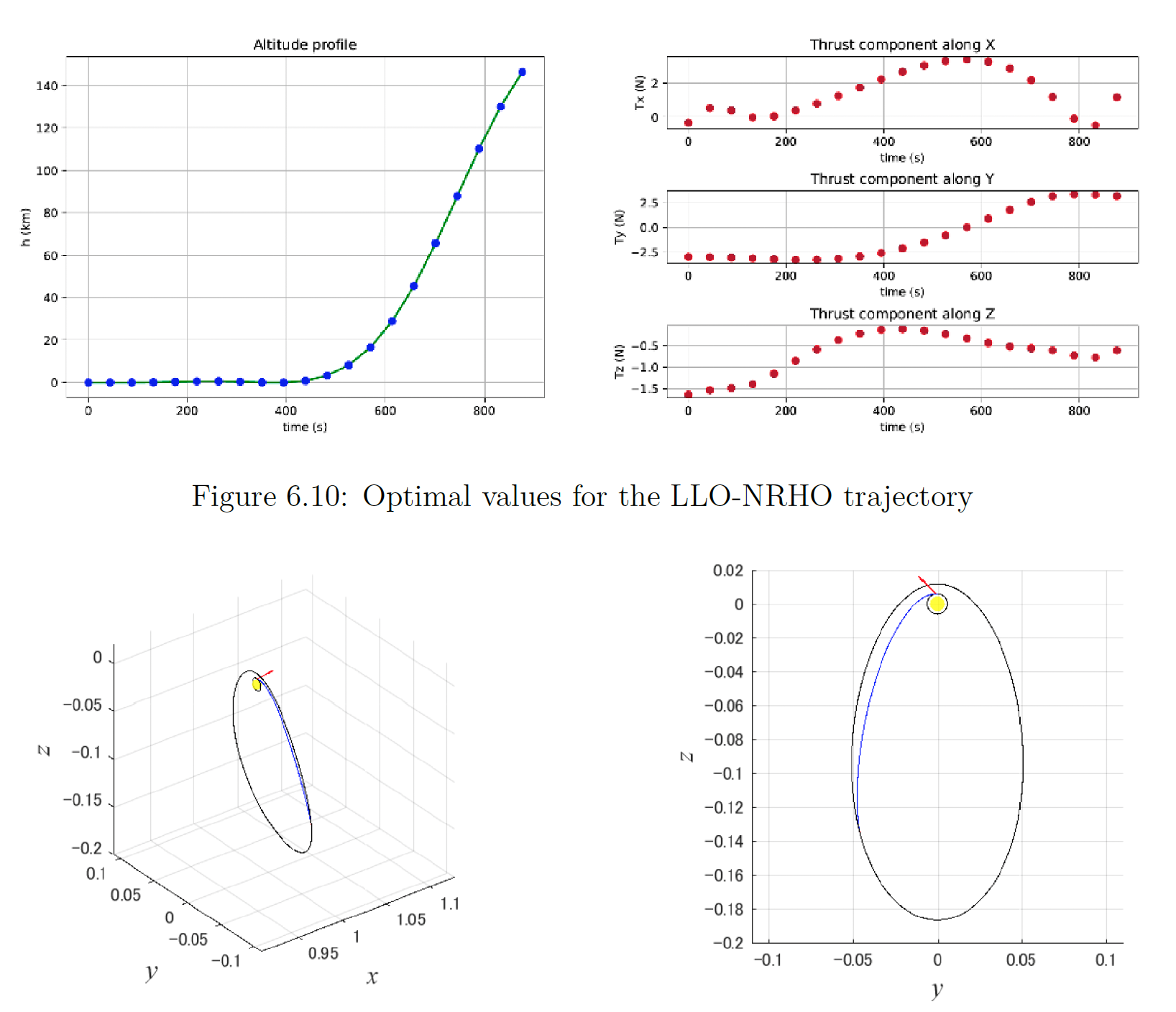
III) LLO-NRHO Rendezvous Trajectory
The last section studies the optimization of rendezvous strategies from LLO to NRHO. The main objective of the optimization is to determine the lunar transfer trajectory from a given LLO to a specific location on the NRHO—in order to perform the rendezvous with the LOP-G— minimizing the fuel consumption (cost function) while satisfying at the same time the imposed constraints on the problem. Insights from the previous mission analysis (e.g. most suitable optimization methods, transcription laws, etc.) will be used in order to determine the best strategy to approach the rendezvous operations.
Following the general 4-step optimization process, the general approach to the OCP3 can be stated according to equations OCP4. For this case, the dynamics of the motion will be described according to the Equations of Motion of the CR3BP EOM (3.22).
Simulating the trajectory from LLO to NRHO in OpenMDAO (without optimizing anything yet), the transfer depicted in figure below is obtained. From this initial guess, it will be possible to compute the optimization problem OCP4. In order to do this, we will use first a shooting method approach, which according to the results previously obtained for the lunar ascending and descending trajectories, it offers much more % convergence effectivity and has less dependency on the initial guess.
The process of refining the initial conditions for both approaches, the initial LLO to HEO and the successive shooting method from LLO to NRHO, required a lot of iterations and combinations of collocation points segments. The converged results for the final approach using collocation methods are shown below, obtaining a TOF of 683s and Mass ratio of 0.53.
4
Conclusions
CHAPTER
__ FINAL SUMMARY
Conclusions
This study optimized lunar trajectories between the lunar surface and Near Rectilinear Halo Orbits (NRHO), comparing various coordinate systems, optimization methods, and mission strategies.
Key Findings:
Coordinate Systems: Polar coordinates showed the highest convergence efficiency (30% higher) for 2D cases but had limited applicability. In 3D, spherical coordinates outperformed Cartesian, achieving 50% better convergence rates and 25% faster results.
Optimization Methods: Shooting methods had higher convergence rates (20-40% improvement) and lower initial guess dependency, making them ideal for short-time simulations. Collocation methods, though more precise (≤10% error), had longer convergence times (+15%) but suited long-term simulations better. Gauss-Lobatto collocation outperformed Radau pseudospectral methods in convergence speed.
Mission Comparisons: One-phase lunar trajectories were more fuel-efficient (10% higher convergence, 25% faster) than two-phase trajectories, which required additional computation and led to increased fuel consumption but improved mission safety.
Trajectory Optimization: One-phase ascent achieved a Time of Flight (TOF) of 3,572s with a Mass Ratio (MR) of 0.67, while descent took 4,431s with an MR of 0.76. Two-phase scenarios consumed more fuel but enhanced mission constraints and safety.
Rendezvous Strategies: A hybrid approach—using shooting methods for initial guesses and collocation for precision—achieved ~10% convergence rates with ≤10% trajectory error. However, convex optimization emerged as a superior alternative, offering higher convergence rates without reliance on initial guesses.
In conclusion, while traditional optimization methods provided reliable results, convex optimization showed potential for higher efficiency and accuracy in lunar trajectory planning.